Near-Infrared
Spectroscopy
By Clare Elwell and Jem
Hebden
Introduction
All of us are exposed to optical (i.e.
visible and near-infrared) radiation from the sun and other sources
throughout our lives. Assuming our eyes are shielded from excessive
intensity, and our skin is protected from the ultraviolet content of
sunlight, we accept this exposure in the knowledge that it is
perfectly safe. Unlike x-rays, optical photons are insufficiently
energetic to produce ionisation, and unless light is concentrated to
such a high degree that it causes burning to the skin, optical
radiation offers no significant hazard. The diagnostic potential of
optical methods has been widely known since Jöbsis [1] first
demonstrated that transmittance measurements of near-infrared (NIR)
radiation could be used to monitor the degree of oxygenation of
certain metabolites. This led to the development and increasingly
widespread use of clinical near-infrared spectroscopy (NIRS), which
offers a safe, non-invasive means of monitoring cerebral function at
the bedside without the use of radioisotopes or other contrast
agents [2].
Human tissues contain a variety of
substances whose absorption spectra at NIR wavelengths are well
defined, and which are present in sufficient quantities to
contribute significant attenuation to measurements of transmitted
light. The concentration of some absorbers, such as water, melanin,
and bilirubin, remain virtually constant with time. However, some
absorbing compounds, such as oxygenated haemoglobin (HbO2), deoxyhaemoglobin (Hb), and oxidised
cytochrome oxidase (CtOx), have concentrations in tissue which are
strongly linked to tissue oxygenation and metabolism. Increasingly
dominant absorption by water at longer wavelengths limits
spectroscopic studies to less than about 1000 nm. The lower limit on
wavelength is dictated by the overwhelming absorption of Hb below
about 650 nm. However, within the 650-1000 nm window, it is possible
with sensitive instrumentation to detect light which has traversed
up to 8 cm of tissue.
Absorption
The absorption of light intensity in a
non-scattering medium is described by the Beer-Lambert Law. This law
states that for an absorbing compound dissolved in a non-absorbing
medium, the attenuation (A) is proportional to the
concentration of the compound in the solution (c) and the
optical pathlength (d):
A
= log10 [Io/I]
= a.c.d ,
where A is the attenuation
measured in optical densities, Io is
the light intensity incident on the medium, I is the light intensity
transmitted through the medium, a is the specific extinction
coefficient of the absorbing compound measured in micromolar per cm,
c is the concentration of the absorbing compound in the
solution measured in micromolar, and d is the distance
between the points where the light enters and leaves the medium. The
product ac is known as the absorption coefficient of
the medium µa. In a medium
containing several different absorbing compounds (except at very
high concentrations not usually met in biological media) the overall
extinction coefficient is simply the linear sum of the contributions
of each compound:
A
= log10 [Io/I] = [ a1.c1
+ a2.c2+ a3.c3
+ ... + an.cn ] d .
A compound which absorbs light in the
spectral region of interest is known as a chromophore. Each
chromophore has its own particular absorption spectrum which
describes the level of absorption at each wavelength. The principle
chromophores in tissue are as follows:
i) Water
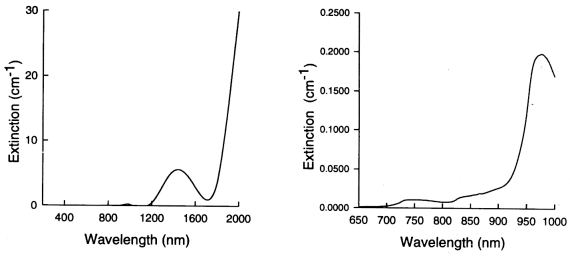
Figure 1: The
absorption spectra of pure water.
As shown above in figure 1, the
absorption of light by water is relatively low between 200 - 900 nm.
Beyond 900 nm absorption starts to rise with increasing wavelength,
a spectral peak being visible at 970 nm. The high concentration of
water in living tissue, typically 80% in adult brain tissue [3],
(equivalent to 56 molar) determines the wavelength region in which
spectroscopic interrogation of tissue is possible by strongly
limiting the tissue thickness through which light can penetrate. For
this reason, the water spectrum is said to demonstrate a "window" of
transparency between 200 and 900 nm within which spectroscopic
measurements can be made. For the purposes of most clinical
measurements the water concentration in tissue can be thought of as
constant, and as such water acts as a fixed constant
absorber.
ii) Lipids
Although the distribution of lipid in
tissue is dependent upon tissue type, it can also be thought of as a
constant absorber with changes in its concentration throughout the
course of a clinical measurement being unlikely. The absorption
spectrum of lipid is approximately the same as that of water and it
can comprise 10 - 40 % (i.e. several molar) of tissue.
iii)
Melanin
Melanin, found in the epidermis layer
of skin, is a highly effective absorber of light, especially in the
ultraviolet region of the spectrum. Although this absorption can be
considered to be constant and oxygen independent, the concentration
of melanin in tissue will directly effect the reflectance of light
from the skin and therefore the transmission of light into the
tissue below.
iv)
Haemoglobin

Figure 2: The
absorption spectra of HbO2 and Hb.
Figure 2 above shows the specific
extinction coefficients of oxygenated haemoglobin (HbO2) and deoxyhaemoglobin (Hb) in the wavelength
range 450 - 1000 nm [4]. The difference in the absorption spectra
explains the well recognised phenomena of arterial blood (containing
approximately 98% HbO2) having a
bright red appearance while venous or deoxygenated blood appears
more blue. In the NIR region of the spectrum the absorption of both
chromophores decreases significantly compared to that observed in
the visible region. However the absorption spectra of Hb and
HbO2 remain significantly different
in this region allowing spectroscopic separation of the compounds to
be possible using only a few sample wavelengths. An isobestic point
where the specific extinction coefficients of the two compounds are
equal can be seen at around 800 nm, which can be used to calculate
haemoglobin concentration independent of oxygen saturation. The
typical value for haemoglobin concentration in, for example, adult
brain tissue is 84 micromolar.
There are other haemoglobin compounds
which have a characteristic absorption in the near infrared,
although their concentrations in tissue are low and in many cases
almost non existent in normal blood. These compounds include
carboxyhaemoglobin, (HbCO), which may be present in significant
quantities in the tissue in some subjects, but has a low specific
extinction coefficient in the NIR rendering its effect on most
in-vivo measurements negligible. Haemiglobin (Hi) is present in very
low concentrations and sulfhaemoglobin (SHb) is not present at all
in normal blood. The combined error in ignoring these compounds in
the measurement of the total haemoglobin signal is probably less
than 1% in normal blood and in the majority of clinical conditions
encountered. However it is worth remembering that some of these
forms of haemoglobin, especially Hi, may become significantly raised
in some diseases of the liver or in malaria.
v) Cytochrome c
oxidase
Cytochrome oxidase (CtOx) is the
terminal enzyme in the cellular respiratory chain, and is located in
the mitochondrial membrane. The enzyme contains four redox active
groups, two haem iron (a and a3) and two copper (CuA and CuB)
centres. These four metal centres change their redox state (i.e.
accept or donate electrons) during electron turnover of the enzyme.
The oxygen binding site of the enzyme is the binuclear unit which is
formed of the CuB and haem
a3. It is the donation of
electrons from this unit to oxygen which accounts for the great
majority of oxygen consumption in biological tissue. The
CuA and haem a centres donate
electrons to this binuclear unit and are therefore not directly
involved in reduction of oxygen. However absorption of NIR radiation
by cytochrome oxidase occurs primarily at the CuA centre, the oxidised spectrum having a
characteristic shape, with a broad peak centred around 830 nm which
is missing in the reduced enzyme. In the short term the total tissue
CtOx concentration does not vary and NIRS measurements of changes in
CtOx thus measure alterations in the redox state concentration of
CuA within cytochrome
oxidase.
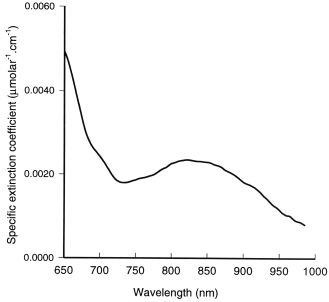
Figure 3: The
difference absorption spectrum between the oxidised and reduced
forms of CtOx.
Since the total CtOx concentration does
not alter, NIRS measurements need only be made of the change
in redox state, so it is only necessary to know the
difference spectrum between the oxidised and reduced forms of
the enzyme. This difference spectrum is shown in figure 3. It can be
seen that the magnitude of the specific extinction coefficients are
similar to those of haemoglobin, but since the concentration of
cytochrome oxidase in living tissue is usually at least an order of
magnitude below that of haemoglobin [5], the measurement of
cytochrome oxidase with optical techniques is by no means as easy as
that of haemoglobin. When oxygen limits the rate of oxygen
consumption by cytochrome oxidase, the CuA centre becomes more reduced. Therefore the
absorbance of NIR light by cytochrome oxidase may be used as an
indicator of oxygen availability at a cellular level and ultimately
of cell metabolism.
Scattering
Scatter of light in tissue is due to
the chaotic variation in refractive index at a microscopic and
macroscopic scale. This occurs at membrane boundaries of the cells
themselves as well as at boundaries between various organelles
inside the cell. Index mismatching will occur between intra and
extracelluar fluid, or intracellular fluid and fluid inside the
nucleus of the cell or other enclosed particles such as
mitochondria, ribosomes, fat globules, glycogen and secretory
globules. As with absorption, the volume of a particular scatterer
within the tissue is as important as its scattering ability.
Evidence suggests that cell membranes are the most important source
of scattering in brain tissue since they account for a large
proportion of the solid content of the tissue.
Scatter is by far the most dominant
tissue-photon interaction at NIR wavelengths. The effect of
scattering is to substantially increase the pathlength travelled by
photons within tissue, and therefore significantly increase the
probability of absorption occurring. When NIR radiation is scattered
in tissue virtually all the collisions are elastic, and the
direction in which the scattered photon travels is dependent upon
the size of the scattering particle, the wavelength of the light,
and the refractive indices of the scattering media through which it
is travelling.
The attenuation (A) due to
single scattering is proportional to the number density of
the scattering particles (N), the scattering cross section of
the particles (s) and the optical pathlength (d):
A
= log10 [Io/I]
= N.s.d .
The product Ns is known as the
scattering coefficient of the medium (µs), and is the probability per unit length of a
photon being scattered. The reciprocal is the mean free path between
scattering events. The scattering coefficients of human tissues are
generally within the range 10 - 100 mm-1, roughly one hundred times greater than
those for absorption [6]. The most highly scattering tissues include
bone, cerebral white matter, and skin dermis.
For multiply scattering media such as
tissue, the simple formula given above no longer applies. In order
to fully describe scatter of light in tissue, it is necessary to
consider the probability of a photon being scattered in a given
direction at each interaction. The probability of a photon, incident
along a unit vector p being scattered into a direction
q is described by the phase function
f(p,q). For a random medium it can be assumed
that this probability is independent of p and only depends on
the angle between the incident and scattered directions, e.
Thus the phase function can be conveniently expressed as a function
of the scalar product of the unit vectors in the initial and final
directions, which is equal to the cosine of the scattering angle
cos(e). The anisotropy in the probability distribution is
commonly characterised in terms of the mean cosine of the scattering
angle g.
In biological tissues, scatter occurs
principally in a forward direction, corresponding to an anisotropy
in the range 0.69 >g >0.99 [6]. Despite the forward
scatter, typical values of scattering coefficient ensure that light
travelling through more than a few millimetres of tissue loses all
of its original directionality, and can be treated as effectively
isotropically distributed. Thus it is convenient to express the
characteristic scatter of tissues in terms of a transport scatter
coefficient:
µs´ = µs (1 - g) ,
which represents the effective number
of isotropic scatters per unit length, and is a fundamental
parameter in diffusion theory.
The
Modified Beer-Lambert Law
When a highly scattering medium is
considered, the Beer-Lambert relationship must be modified to
include (i) an additive term, G, due to scattering losses and
(ii) a multiplier, to account for the increased optical pathlength
due to scattering. The true optical distance is known as the
differential pathlength (DP) and the scaling factor as the
differential pathlength factor (DPF):
DP
= DPF . d ,
where d is the geometrical
distance. The modified Beer-Lambert law which incorporates these two
additions is then expressed as:
A
= log10 [Io/I] = a.c.d. DPF +
G .
Unfortunately G is unknown and
is dependent upon the measurement geometry and the scattering
coefficient of the tissue interrogated. Therefore this equation
cannot be solved to provide a measure of the absolute
concentration of the chromophore in the medium from a measure of
absolute attenuation. However if G does not change
during the measurement period, it is possible to determine a
change in concentration (c2-c1) of
the chromophore from a measured change in attenuation
(A2-A1):
(A2-A1)
= (c2-c1).a.d. DPF .
Note that the differential
attenuation is actually measured, giving rise to the terminology
differential pathlength and differential pathlength
factor. The quantification of the change in concentration still
depends upon the measurement of the geometrical distance d
and the differential pathlength factor, i.e. the true optical
pathlength which the scattered light has travelled. Although
d is simple enough to measure, as it is purely the
geometrical distance between the points where the light enters and
leaves the medium, determination of DPF is more difficult. There are
a number of different techniques which can be used to measure DPF in
tissue, as briefly described in the following section.
Measurements of DPF
a) Time of Flight
Method
The development of picosecond pulse
lasers and ultrafast detectors during the past twenty years has made
possible the direct measurement of the time of flight of light
through tissue [7]. The system currently used at University College
London is a Ti:sapphire laser pumped by a diode-pumped CW laser. The
system can produce a single pulse with a duration of approximately 2
ps, and with suitable mirrors the laser can be tuned between 740 nm
and 920 nm. The laser beam is split and part of the laser output is
taken directly to the streak camera as a time reference. The other
part of the beam is directed through the tissue sample. The temporal
reference and the signal which has traversed the tissue sample are
recorded simultaneously on the same streak image. The geometrical
distance d between the centre of the transmitting fibre and
the centre of the detecting fibre bundle is accurately measured. As
with conventional spectroscopy measurements, it is important to
minimise movement of the tissue between the fibres and various
stereotactic devices have been used to stabilise the tissue under
interrogation.
The time difference <t> between
the light entering the tissue and the mean time of that which has
traversed the tissue is measured from the streak image and is then
used in the calculation of the differential pathlength factor in a
simple time of flight approximation:
DPF
= DP / d = cv.< t> / d.n ,
where cv is the speed of light in a vacuum, and
n is the refractive index of the tissue (usually taken as
1.40 [8]). Time of flight systems of the type described above are
large, expensive, and confined to dedicated optical laboratories,
which precludes routine clinical use on neonates. To date therefore,
this method has generally been restricted to measurements on post
mortem infants and on adult volunteers [9-11].
b) Intensity Modulated
Optical Spectrometer
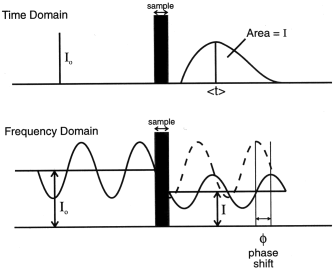
Figure 4: Measurement in the time and
frequency domains.
When NIRS is applied to measurements of
tissue oxygenation in the fetal head during labour and childbirth or
in muscles during exercise, large changes in the geometrical
distance d may occur during a study. The ultimate goal of a
reliable accurate bedside spectrometer can therefore only
realistically be achieved when real time measurement of the
total light path can be incorporated. By making spectroscopy
measurements in the frequency rather than the time domain, it has
been possible to develop a new method of continuously monitoring the
total path which the NIR light has travelled in the tissue of
interest. Figure 4 demonstrates schematically the principles of the
time and frequency domain measurements of DPF. A continuous laser
source can be easily modulated at all frequencies from DC to a few
hundred MHz and the phase shift between the light entering and
exiting the tissue can be recorded. It has been shown [12] that if
P is the phase shift measured in radians, then for modulation
frequencies less than 200 MHz, the total distance travelled through
the tissue, DP, is given by:
DP
= P. cv / 2.pi.
f. n ,
where f is the modulation
frequency. Optical pathlengths at one or two wavelengths have been
reported from a measurement of phase shift of light modulated at a
single frequency of 220 MHz [13].
An intensity modulated optical
spectrometer capable of working at several wavelengths and over a
wide range of modulation frequencies has been developed at UCL for
use in a number of clinical studies [14-16]. In this spectrometer
four intensity modulated laser diode sources produce light in the
NIR region enabling the user to measure the optical pathlength at
each wavelength and simultaneously perform the conventional
spectroscopy measurements for determining the change in
concentration of Hb, HbO2 and CtOx.
In this way the change in measured attenuation can be corrected for
pathlength variations in real time. Since the distance measured is
the total optical pathlength, DP, this instrument negates the need
for manual measurement of the geometric distance d, and
therefore represents a dramatic improvement in the accuracy of
pathlength and spectroscopy measurements. Research with this type of
instrument will prove useful not only in studies where the optical
fibres are likely to move (e.g. during fetal measurements or
exercise studies) but also in improving the accuracy of oxidised
cytochrome oxidase measurements which, due to the chromophore's
relatively low concentration in tissue are particularly vulnerable
to errors in optical pathlength estimation. In addition, since this
type of system is capable of measuring DP at four wavelengths, a
more accurate correction for the pathlength variations known to
occur with absorption coefficient, µa, (and hence wavelength) can also be made.
Although this type of system allows a
continuous measurement of DP combined with the normal spectroscopic
measurements, the first clinical application of the instrument has
been to collect data on the absolute values of DP in different
groups of subjects. If the geometrical distance d is measured
at the time of the study, the DPF can easily be calculated from the
DP measurement, and compared with previously recorded values. The
portable nature of the instrument has also allowed the measurement
of cranial DPF to be made on a large group of live neonates at the
cotside [15]. In addition a study has recently been completed to
investigate the age dependence of cranial DPF in humans. The
intensity modulated spectrometer described above was used to measure
cranial DPF in a total of 283 subjects whose age ranged from 1 day
to 50 years [16]. The results suggest a slowly varying age
dependence of DPF following the relation:
DPF780 = 5.13 + 0.07Y 0.81 ,
where DPF780 is the differential
pathlength factor at 780 nm and Y is the age of the subject
in years.
Factors influencing the total optical
pathlength
It has been shown that DP is dependent
upon the following factors:
a) Tissue
Type
Measurements of DPF have been made on
neonatal head, and adult head, forearm and calf. A marked difference
is seen between these four tissue types. This difference is to be
expected since the DPF is directly dependent upon the proportion of,
for example, soft tissue, muscle and bone in the illuminated
tissue.
b) Absorption
coefficient (and wavelength)
The time of flight system has been used
to demonstrate the relationship between DPF and wavelength (and
hence absorption coefficient) in the adult head, forearm and calf
(in vivo) and the infant head [17]. The DPF was estimated
from mean time of flight measured between 740 nm and 840 nm. In all
tissues the DPF generally decreased with increasing wavelength,
although also exhibiting the absorption characteristics of
haemoglobin, with a variation of typically 12% over the wavelength
range. For this reason it is always important when quoting DPF
values to also quote the wavelength at which the DPF measurements
have been made. The spectral dependence of DPF must also be taken
into account in the algorithm used to convert from attenuation (OD)
data at a range of wavelengths to changes in chromophore
concentration.
c) Geometry of
Optodes
It has been demonstrated [18] with the
aid of computer simulation, that on a spherical object DPF is
dependent upon angular position. DPF may vary significantly between
an emitter-detector angle of 180 to 60 degrees, and even more
rapidly for lesser angles. In contrast, an experimental study [10]
showed that in all tissues DPF initially falls with increasing
geometrical distance, d, the value becoming almost constant
for source-detector spacings above 2.5 cm. This discrepancy between
the theoretical and experimental results can be explained in part by
the fact that the theoretical model did not take into account the
inhomogeneity of the tissue illuminated. This has been confirmed by
modelling of multilayered tissues where the DPF has been shown to
vary with angle in the same way as that observed experimentally
[19]. Much work is currently being done to further refine the
methods used for prediction of DPF, particularly in realistic tissue
models [20].
Spectroscopic Measurements of the
Brain
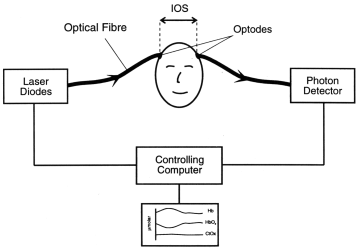
Figure 5: NIRS
measurement across the head.
Figure 5 shows a schematic of the
experimental set up for the spectroscopic measurement across a head.
The optical fibres which carry the NIR light to and from the head
are terminated with small prisms which direct the light normally on
to the surface of the tissue. The geometrical distance d,
known as the interoptode spacing (IOS), is usually measured
with a pair of callipers directly over the measurement site. Note
this distance is the chord (straight line) distance rather than the
length of the arc between the two points. This assumption is based
upon the fact that light inside the brain becomes essentially
diffuse within a few millimetres of entering the tissue, at which
point it becomes an isotropic source [18], even if the angle between
the source and detector is less than 180 degrees.
The differential pathlength factor has
been measured in the adult head using both the UCL time of flight
system and the UCL intensity modulated optical spectrometer, and a
value of approximately 6 was obtained. Therefore, for an IOS of 4
cm, the mean distance which the light actually travels in the head
is approximately 24 cm.
The chromophores of interest within the
tissue, whose concentration vary with oxygenation are HbO2, Hb and CtOx. The specific extinction
coefficients (a) for these chromophores are expressed in
units of per micromolar of chromophore per litre of tissue per cm.
Once d, a and DP are known the change in
chromophore concentration can easily be computed from the measured
change in attenuation. However for the simultaneous
computation of the changes in concentration of a number of
chromophores from the changes in attenuation at a number of
wavelengths, a matrix operation must be performed incorporating the
relevant extinction coefficients for each wavelength and
chromophore. For each wavelength it is assumed that the linear
changes in attenuation for each chromophore can be linearly summed.
The result of these computations is the value of the absolute
change in concentration of each chromophore in the non
arbitrary units of micromolar of chromophore per litre of
tissue.
Since the absolute concentration of
chromophore is unknown (and cannot be determined due to the effects
of light scattering within the tissue), all measurements are
expressed as absolute concentration changes from an arbitrary
zero at the start of the measurement period. Thus using this
technique the quantified changes in tissue oxygenation can be non
invasively monitored. Furthermore the quantified changes in the
concentration of Hb and HbO2 in the
units micromolar can be used to measure absolute haemodynamic
parameters such as cerebral blood flow [21] and cerebral blood
volume [22].
References
- Jöbsis, FF (1977): Science 198,
1264-1267.
- Cope, M, and Delpy DT (1988): Med. & Biol.
Eng. & Comput. 26, 289-294.
- Woodard, HQ, and White, DR (1986): Br. J.
Radiol. 59, 1209-1219.
- Horecker, BL (1943): J. Biol. Chem. 148,
173-183.
- Sato, N, Hagihara, B, Kamada, T, and Abe, H
(1976): Anal. Biochem. 74, 105-117.
- Cheong, W-F, Prahl, S, and Welch, AJ (1990):
IEEE J. Quant. Electron. 26, 2166-2185.
- Delpy, DT, Cope, M, van der Zee, P, Arridge,
SR, Wray, S, and Wyatt JS (1988): Phys. Med. Biol. 33,
1433-1442.
- Bolin, FP, Preuss, LE, Taylor, RC, and Ference,
R (1989): Appl. Opt. 28, 2297-2302.
- Wyatt, JS, Cope, M, Delpy, DT, van der Zee, P,
Arridge, SR, Edwards, AD, and Reynolds, EOR (1990): Dev.
Neuroscience 12, 140-144.
- van der Zee, P, Cope, M, Arridge, SR,
Essenpreis, M, Potter, LA, Edwards, AD, Wyatt, JS, McCormick, DC,
Roth, SC, Reynolds, EOR, and Delpy, DT (1992): Adv. Exp. Med.
& Biol. 316, 143-153.
- Essenpreis, M, Cope, M, Elwell, CE, Arridge,
SR, van der Zee, P, and Delpy, DT (1993): Adv. Exp. Med. &
Biol. 333, 9-20.
- Arridge, SR, Cope, M, and Delpy, DT (1992):
Phys. Med. Biol. 37, 1531-1560.
- Weng, J, Zhang, MZ, Simons, K, and Chance, B
(1991): Proc. SPIE 1431, 161-170.
- Duncan, A, Whitlock, T, Cope, M, and Delpy, DT
(1993): Proc. SPIE 1888, 248-257.
- Duncan, A, Meek, JH, Clemence, M, Elwell, CE,
Tyszczuk, L, Cope, M, and Delpy, DT (1995): Phys. Med. Biol.
40, 295-304.
- Duncan, A, Meek, JH, Clemence, M, Elwell, CE,
Fallon, P, Tyszczuk, L, Cope, M, and Delpy, DT (1996): Pediatr.
Res. 39, 889-894.
- Essenpreis, M, Elwell, CE, Cope, M, van der
Zee, P, Arridge, SR, and Delpy, DT (1993): Appl. Opt. 32,
418-425.
- van der Zee, P, Arridge, SR, Cope, M, and
Delpy, DT (1990): Adv. Exp. Med. & Biol. 277, 79-84.
- Hiraoka, M, Firbank, F, Essenpreis, M, Cope, M,
Arridge, SR, van der Zee, P, and Delpy, DT (1993): Phys. Med.
Biol. 38, 1859-1876.
- Schweiger, M, Arridge, SR, and Delpy DT (1993):
J. Math. Imag. & Vision 3, 263-283.
- Edwards, AD, Richardson, C, Cope, M, Wyatt, JS,
Delpy, DT, and Reynolds, EOR (1988): Lancet 2, 770-771.
- Wyatt, JS, Cope, M, Delpy, DT, Richardson, CE,
Edwards, AD, Wray, SC, and Reynolds, EOR (1990): J. Appl. Physiol.
68, 1086-1091.
Click here
for some useful references on near-infrared spectroscopy and related
topics.
Return
to BORL Research Topics.
Return
to BORL Homepage.
![]() +44 (0)20 7679 0200 - Copyright © 1999-2005 UCL
+44 (0)20 7679 0200 - Copyright © 1999-2005 UCL